Constrained Utility Maximization

Utility maximization is the process of choosing the option that provides the highest level of utility, given a set of available options and the individual’s preferences. It involves evaluating each option using a utility function and selecting the one that maximizes the utility subject to constraints.

Outline

• Optimal rational choices are based on the assumption that individuals have clear preferences ranked by a utility function and can evaluate the costs and benefits associated with each choice. Optimal rational choices involve selecting the option that maximizes the utility, i.e., the satisfaction derived from the decision, while considering constraints such as budgets.

• The role of income and prices. Understanding the impact of income and prices on decision-making is crucial in comprehending the rationale behind the actions taken by decision makers. By studying the correlation between income, prices, and utility maximization within a budget constraint, we can gain valuable insights into consumer behavior, resource allocation, and market dynamics.

---

Optimal rational choices

An optimal rational decision-making agent maximizes its utility function, i.e., the agent searches for a combination of goods and services that gives the highest satisfaction subject to various constraints, e.g., a budget constraint (Definition 3):

Definition 3 (Maximum utility and budget constraints)

An agent has a set of \(n\) objects \(X = \left\{x_{i}\right\}_{i=1}^{n}\), a utility function \(U:X\rightarrow\mathbb{R}\), and a total of \(I\) units of resource to allocate, e.g., money, time, etc. An optimal rational agent maximizes its utility subject to its resource budget:

\[\begin{split} \begin{eqnarray} \text{maximize}~\mathcal{O} &=& U\left(x_{1},\dots,x_{n}\right) \\ \text{subject to}~\sum_{i\in{1,\dotsc,n}}c_{i}x_{i} & = & I\\ \text{and}~x_{i}&\geq&{0}\qquad{i=1,2,\dots,n} \end{eqnarray} \end{split}\]

The quantity \(c_{i}\geq{0}~\forall{i}\) denotes the cost of object \(i\), and \(x_{i}\geq{0}\) represents the amount of object \(i\) purchased or consumed by the agent.

The problem in Definition 3 can be solved for the unknown consumption levels of \(x_{i}\) using various techniques.

Resource constraints

To manage resources effectively, you need to prioritize your expenses, make trade-offs, and find the best ways to use what you have, such as time, money, and people. These limitations come from the fact that resources are finite and scarce, so you need to plan carefully and allocate them wisely to meet your needs and goals.

In the context of optimal decision problems, we represent the utilization of scarce resources using budget constraints. Budget constraints are a mathematical representation of the trade-offs between two or more goods or services brought about by resource limitation (Definition 4):

Definition 4 (Budget constraint)

Let \(I\geq{0}\) denote a scarce resource, e.g., time, money, etc., that is allocated to consume, purchase, etc., the set of \(n\) objects \(X = \left\{x_{i}\right\}_{i=1}^{n}\). The budget constraint for the set \(X\) is given by:

\[ \begin{equation} \sum_{i\in{1,\dotsc,n}}c_{i}x_{i} = I \end{equation} \]

The terms \(x_{i}\geq{0}\) denote the quanity of object \(i\) consumed, purchased, etc, and \(c_{i}\geq{0}\) denotes the unit cost of object \(i\).

Two goods: Apples and Oranges

Let’s consider a case where we have the budget \(I\), and two goods X = {apples, oranges}. In this case, the budget constraint is a line in the apples versus oranges plane (Fig. 5).

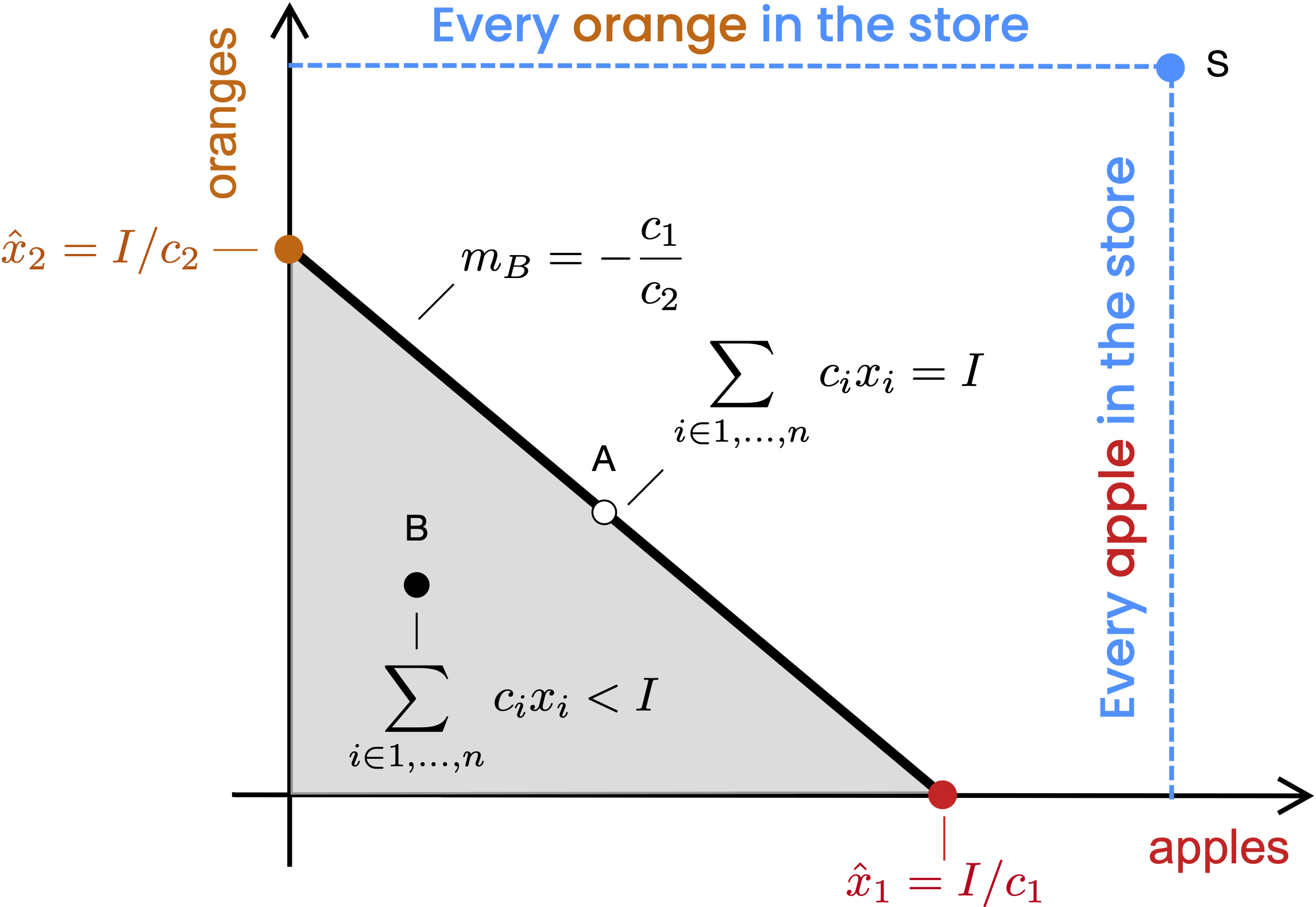
Fig. 5 Two-dimensional budget constraint for the X = {apples, oranges} set of goods.

There are some interesting points to note about the budget constraint shown in Fig. 5:

• The slope of the resource constraint line \(m_{B}\) is the negative ratio of the unit costs of apples and oranges.

• Point S represents the maximum number of apples and oranges that can be purchased at the store (supply constraint).

• The intercepts \(\hat{x}_{1}\) and \(\hat{x}_{2}\) indicate the maximum amount of apples and oranges that can be bought based on the budget constraint and the price of each fruit. For instance, \(\hat{x}_{1}\) refers to the maximum number of apples that can be bought, while \(\hat{x}_{2}\) refers to the maximum number of oranges that can be purchased.

• Any point on the budget constraint line, such as point A, represents a potential combination of apples and oranges that can be purchased that exactly satisfies the budget constraint.

• Any point within the gray area, such as point B, also represents a possible combination of apples and oranges that can be purchased, but there will be leftover resources, such as money.

The objective is to determine the best combination of apples and oranges that maximizes the utility function and exactly satisfies the budget. This means finding the point on the budget constraint line that offers the highest utility.

Lagrange multipliers and utility maximization

Let’s begin with a classical approach, the method of Lagrange multipliers. The method of Lagrange multipliers introduces additional variables, called Lagrange multipliers, which integrate the constraints into a modified objective function called the Lagrangian (Definition 5):

Definition 5 (Method of Lagrange multipliers)

To find the optimum of a function \(f(x)\) subject to the equality constraint \(g(x)\), we form the Lagrangian \(\mathcal{L}(x,\lambda)\):

\[ \begin{equation} \mathcal{L}(x,\lambda) = f(x) + \lambda\cdot{g}(x) \end{equation} \]

where \(\lambda\) is the Lagrange multiplier for constraint \(g(x)\). At a critical point (maximum or minimum), the partial derivatives of the Lagrangian with respect to \(x\) and \(\lambda\) vanish:

\[\begin{split} \begin{eqnarray} \frac{\partial\mathcal{L}}{\partial{x}} & = & f^{\prime}(x) + \lambda\cdot{g^{\prime}(x)} = 0\\ \frac{\partial\mathcal{L}}{\partial{\lambda}} & = & g(x) = 0 \end{eqnarray} \end{split}\]

This system of equations, which represents first-order optimality conditions, can be solved for the critical points and, thus, the maximum or minimum value of the objective function.

The constrained utility maximization problem has the Lagrangian:

\[ \begin{equation*} \mathcal{L}(x,\lambda) = U(x_{1},\dots,x_{n}) + \lambda\cdot\left(I-\sum_{i\in{1,\dotsc,n}}c_{i}x_{i}\right) \end{equation*} \]

which then gives the system of equations:

\[\begin{split} \begin{eqnarray*} \frac{\partial\mathcal{L}}{\partial{x_{i}}} & = & \bar{U}_{i} - \lambda\cdot{c_{i}} = 0 \qquad{i=1,2,\dots,n} \\ \frac{\partial\mathcal{L}}{\partial\lambda} & = & I - \sum_{i\in{1,\dotsc,n}}c_{i}x_{i} = 0 \end{eqnarray*} \end{split}\]

where \(\bar{U}_{i}\) denotes the marginal utility of good or service \(i\). The system of \(n+1\) equations can be solved to find the optimal consumption levels of \(x_{i}\) and the Lagrange multiplier \(\lambda\).

The secret meaning of Lagrange multipliers

The first \(n\) first-order optimality conditions can be solved to arrive at an expression for the Lagrange multiplier \(\lambda\):

\[\lambda = \frac{\bar{U}_{i}}{c_{i}}\qquad\forall{i}\]

Thus, the Lagrange multiplier is the marginal utility per dollar spent on good \(i\). Further, the Lagrange multiplier provides the basis for the matching condition at the optimum:

\[\frac{\bar{U}_{j}}{c_{j}} = \frac{\bar{U}_{k}}{c_{k}}\qquad\forall{j,k}\]

Cobb-Douglas utility maximization problem

Consider a utility maximization problem with the Cobb-Douglas utility function, \(U(x_{1},x_{2}) = x_{1}^{\alpha}x_{2}^{1-\alpha}\), subject to a budget constraint. The Lagrangian is given by:

\[ \begin{equation*} \mathcal{L}(x,\lambda) = x_{1}^{\alpha}x_{2}^{1-\alpha} + \lambda\cdot\left(I-c_{1}x_{1}-c_{2}x_{2}\right) \end{equation*} \]

which gives the first-order optimality conditions:

\[\begin{split} \begin{eqnarray*} \frac{\partial\mathcal{L}}{\partial{x_{1}}} & = & \alpha\cdot{x_{1}^{\alpha-1}}x_{2}^{1-\alpha} - \lambda\cdot{c_{1}} = 0 \\ \frac{\partial\mathcal{L}}{\partial{x_{2}}} & = & (1-\alpha)\cdot{x_{1}^{\alpha}x_{2}^{-\alpha}} - \lambda\cdot{c_{2}} = 0 \\ \frac{\partial\mathcal{L}}{\partial\lambda} & = & I - c_{1}x_{1} - c_{2}x_{2} = 0 \end{eqnarray*} \end{split}\]

This system can be solved for the optimal consumption levels of \(x_{1}\) and \(x_{2}\). However, it is non-linear. Thus, we often need to use numerical methods to find the optimal values of \(x_{1}\) and \(x_{2}\). The Cobb-Douglas utility function will give a unique optimal solution.

Linear utility maximization problem

Consider utility maximization problem that uses a linear utility function \(U(x_{1},x_{2}) = \alpha_{1}x_{1}+\alpha_{2}x_{2}\) subject to a budget constraint. The Lagrangian for this problem is given by:

(14)\[\mathcal{L}(x,\lambda) = \alpha_{1}x_{1} + \alpha_{2}x_{2} + \lambda\cdot\left(I-c_{1}x_{1}-c_{2}x_{2}\right)\]

which gives the first-order optimality conditions:

(15)\[\begin{split}\begin{eqnarray} \frac{\partial\mathcal{L}}{\partial{x_{1}}} & = & \alpha_{1} - \lambda\cdot{c_{1}} = 0 \\ \frac{\partial\mathcal{L}}{\partial{x_{2}}} & = & \alpha_{2} - \lambda\cdot{c_{2}} = 0 \\ \frac{\partial\mathcal{L}}{\partial\lambda} & = & I - c_{1}x_{1} - c_{2}x_{2} = 0 \\ \end{eqnarray}\end{split}\]

The first-order optimality conditions are \(3\times{3}\) system of linear algebraic equations, which are underdetermined. To see this, let’s perform a rank test. The optimality conditions can be written in matrix-vector form as:

\[\begin{split}\begin{bmatrix} 0 & 0 & -c_{1} \\ 0 & 0 & -c_{2} \\ -c_{1} & -c_{2} & 0 \\ \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ \lambda \\ \end{bmatrix} = \begin{bmatrix} -a_{1} \\ -a_{2} \\ -I \\ \end{bmatrix}\end{split}\]

or \(\mathbf{A}\mathbf{\theta} = \mathbf{b}\) which can (theoretically) be inverted to find the solution if the matrix \(\mathbf{A}\) has full rank:

\[\theta = \mathbf{A}^{-1}\mathbf{b}\]

However, the rank of matrix \(\text{rank}(\mathbf{A}) = 2\), which indicates the system of equations is underdetermined. This means that there are more unknowns than equations, leading to an infinite number of possible solutions.

Solving the system of equations for linear utility maximization

To find a solution to the first-order optimality conditions, we could use the Moore-Penrose pseudo-inverse of the matrix \(\mathbf{A}\). Alternatively, in the two-dimensional case, we find, after some analysis, that the optimal solution depends upon the slope of the budget constraint line, \(m_{B}\) and the slope of the linear indifference curve, \(m_{U}\) Fig. 6:

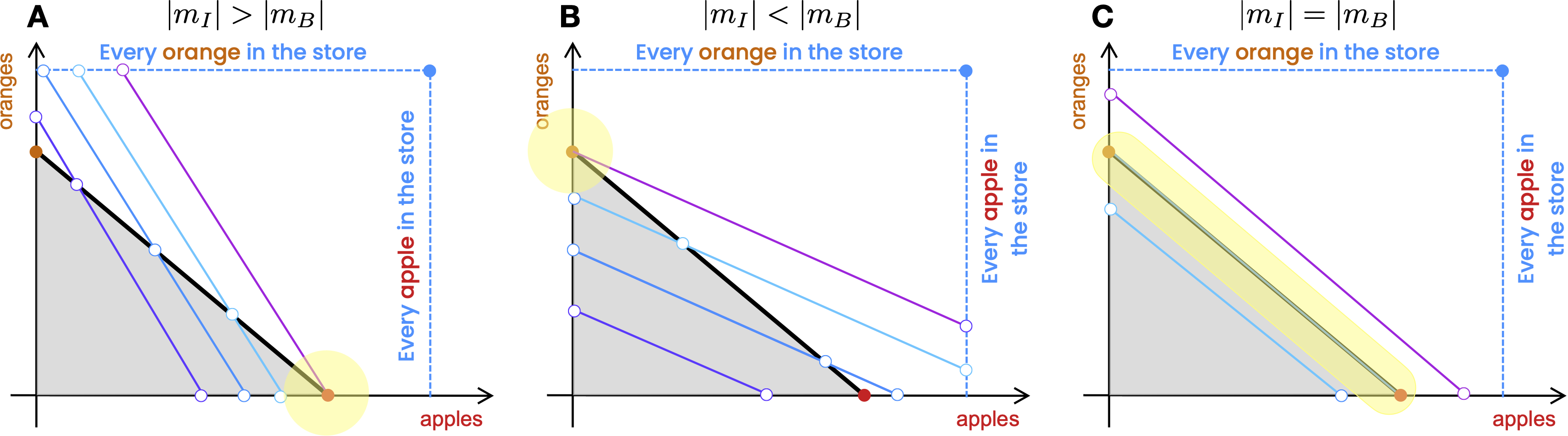
Fig. 6 Solutions of the utility maximization problem with a linear utility function. The yellow regions highlight the optimal solution for each of the cases. The optimal solution depends upon the slope of the budget constraint line, \(m_{B}\) and the slope of the linear indifference curve, \(m_{I}\).

The optimal solution is given by:

• Case A: If \(m_{U} > m_{B}\), the optimal solution is the x-intercept of the budget constraint line, i.e., \(\hat{x}_{1} = \frac{I}{c_{1}}\) and \(\hat{x}_{2} = 0\).

• Case B: If \(m_{U} < m_{B}\), the optimal solution is the y-intercept of the budget constraint line, i.e., \(\hat{x}_{1} = 0\) and \(\hat{x}_{2} = \frac{I}{c_{2}}\).

• Case C: If \(m_{U} = m_{B}\), the optimal solution is any point on the budget constraint line, i.e., any point betweem \(\hat{x}_{1} = \frac{I}{c_{1}}\) and \(\hat{x}_{2} = \frac{I}{c_{2}}\).

Numerical solutions of utility maximization problems

The Cobb-Douglas utility function example above illustrates a case where the first-order optimality conditions are non-linear and not easy to solve analytically. In these cases, which are common, we must use numerical methods to find the optimal values for \(x_{1},\dots,x_{n}\).

We’ll make use of the JuMP and MadNLP packages which provide numerical techniques for solving optimization problems:

• The JuMP package provides a high-level interface for defining optimization problems.

• The MadNLP package is used by JuMP to solve optimization problems, but it can also be used directly to solve constrained optimization problems.

Let’s revisit the Cobb-Douglas utility maximization problem from above, but this time we’ll use JuMP and MadNLP to solve the problem numerically. First, we’ll define a type that represents the problem (and stores useful data about the problem):

mutable struct MySimpleCobbDouglasChoiceProblem <: AbstractSimpleChoiceProblem

    # data -
    α::Array{Float64,1}
    c::Array{Float64,1}
    I::Float64
    bounds::Array{Float64,2}
    initial::Array{Float64,1}

    # constructor
    MySimpleCobbDouglasChoiceProblem() = new();
end

Next, we’ll define a function that takes an instance of the MySimpleCobbDouglasChoiceProblem problem object, solves the constrained utility maximization problem, and returns a dictionary with the results:

"""
    solve(problem::MySimpleCobbDouglasChoiceProblem) -> Dict{String,Any}

Solves the optimal decision problem with a budget constraint with a Cobb-Douglas utility function
"""
function solve(problem::MySimpleCobbDouglasChoiceProblem)::Dict{String,Any}

    # initialize -
    results = Dict{String,Any}()
    α = problem.α;
    c = problem.c;
    bounds = problem.bounds;
    I = problem.I;
    xₒ = problem.initial

    # how many variables do we have?
    d = length(α);

    # Setup the problem -
    model = Model(()->MadNLP.Optimizer(print_level=MadNLP.INFO, max_iter=500))
    @variable(model, bounds[i,1] <= x[i=1:d] <= bounds[i,2], start=xₒ[i]) # we have d variables
    
    # set objective function -   
    @NLobjective(model, Max, (x[1]^α[1])*(x[2]^α[2]));
    @constraints(model, 
        begin
            # my budget constraint
            transpose(c)*x <= I
        end
    );

    # run the optimization -
    optimize!(model)

    # populate -
    x_opt = value.(x);
    results["argmax"] = x_opt
    results["budget"] = transpose(c)*x_opt; 
    results["objective_value"] = objective_value(model);

    # return -
    return results
end

Finally, we’ll put it all together and solve the problem. We build the problem object using the build(...) function, and then call the solve(...) function to estimate the optimal solution:

Listing 7 runme-cobb-douglas.jl

# include the include (load the reqd packages) -
include("Include.jl")

# initialize -
α = [0.55, 0.45]; # coefficients
c = [2.0, 4.0]; # price of x1 and x2

# build my problem object -
problem = build(MySimpleCobbDouglasChoiceProblem, (
    
    initial = 0.1*ones(2), # initial guess
    α = α, # coefficients
    c = c, # price of x1 and x2
    I = 100.0, # income
    
    # how much of x₁ and x₂ can be we buy?
    bounds = [
        0.0 100.0; # L U
        0.0 100.0; # L U
    ]
));

# call tghe solve function. This will return a dictionary -
solution = solve(problem);

The optimal solution for the consumption of good \(x_{1}\) and \(x_{2}\) subject to the budget constraint is a point of tangency between the indifference curve and the budget constraint (Fig. 7):

Fig. 7 Optimal solution for the two-dimensional goods problem assuming a Cobb-Douglas utility function. Parameters: \(\alpha_{1} = 0.55\), \(\alpha_{2} = 0.45\), \(c_{1} = 2\), \(c_{2} = 4\), and \(I = 100\). The optimal combination: \(x_{1}^{*} = 27.5\), \(x_{2}^{*} = 11.25\).

Let’s check the first-order optimality conditions to make sure the solution is optimal:

# specify parameters (and solution) from the problem
α, c₁, c₂, x₁, x₂, I = 0.55, 2.0, 4.0, 27.5, 11.25, 100.0

# compute the marginal utility at the optimum -
Ū₁ = α*(x₁^(α-1))*(x₂^(1-α))
Ū₂ = (1-α)*(x₁^(α))*(x₂^(-α))

# compute the Lagrange multiplier -
λ = Ū₁/c₁;

# Compute the first-order conditions -
E1 = Ū₁ - λ*c₁
E2 = Ū₂ - λ*c₂
E3 = I - (c₁*x₁ + c₂*x₂)

# print -
println("Optimality conditions: $(E1), $(E2), $(E3) with λ = $(λ)")

Optimality conditions: 0.0, -1.1102230246251565e-16, 0.0 with λ = 0.1839295959087945

The role of income and prices

By examining the relationship between income, prices, and utility maximization subject to a budget constraint, we gain valuable insights into consumer behavior, resource allocation, and market dynamics.

---

Summary

In this set of lectures, we discussed optimal rational choices and constrained utility maximization. We learned how to solve constrained utility maximization problems using the Lagrangian method and numerical optimization. We also explored how the optimal solution changes as a function of available income and the prices of goods and services.

• Optimal rational choices are based on the assumption that individuals have clear preferences ranked by a utility function and can evaluate the costs and benefits associated with each choice. Optimal rational choices involve selecting the option that maximizes the utility, i.e., the satisfaction derived from the decision, while considering constraints such as budgets.

• The role of income and prices. Understanding the impact of income and prices on decision-making is crucial in comprehending the rationale behind the actions taken by decision-makers. By studying the correlation between income, prices, and utility maximization within a budget constraint, we can gain valuable insights into consumer behavior, resource allocation, and market dynamics.