Ctrl+K

Expressions, Variables, and Types

Expressions, Variables, and Types#

Expressions and Variables#

Expressions are a combination of values, variables, and operators that evaluate to a single value. A variable is like a box that holds a value, and that value has a type. For example, types can be numbers such as 3, Boolean values like true or false, or text like:

“Your computer is the only thing in the universe that unconditionally loves you, perhaps excluding your mother. Your computer will do anything you ask it to do with no pushback and no attitude. You just need to know how to talk to it!”

However, computers and Humans don’t speak the same language. Humans understand that 3 is an integer, i.e., 3\(\in\mathbb{Z}\), and Julia rocks is text, but the computer doesn’t see these values the same way we do. Expressions are a fundamental building block of most programming languages, and they are used to perform calculations, compare values, and assign values to variables. Here are some common examples of expressions in the Julia programming language:

  • 2 + 3: This expression evaluates to the value 5, an integer.

  • x * y: This expression evaluates to the product of the variables x and y, which are assumed to be numbers. However, x and y can be other types, e.g., text, and the * operator will perform a different operation, e.g., string concatenation.

  • x == y: This expression evaluates to true if x and y are equal and false if they are not; true and false are Boolean types, i.e., true\(\in\mathbb{B}\) and false\(\in\mathbb{B}\) where \(\mathbb{B} = \left\{\text{true}, \text{false}\right\}\).

  • x > y: This expression evaluates to true if x is greater than y and false if it is not; true and false are Boolean types. This statement assumes x and y are numbers. However, x and y can be other types. For example, if they are text, the > operator will perform a different operation, e.g., lexicographic comparison.

  • x = 3: This expression assigns the value 3 to the variable x.

Expressions are evaluated to a value that has a type. For example, the expression 2 + 3 evaluates to the value 5, an integer. The expression x = 3 assigns the value 3 to an integer variable x. The expression x == y evaluates to true or false, which are Boolean values. The expression x * y evaluates to the product of the variables x and y, which are assumed to be numbers. However, x and y can be other types, e.g., text, and the * operator will perform a different operation, e.g., string concatenation.

Numerical and Logical Data Types#

For a computer, everything is a binary number, i.e., numbers written to the base 2. From this perspective, integers are binary numbers, text is a set of binary numbers, Boolean values are binary numbers, etc. In many traditional programming languages, it is required to declare the variable type before using it so that the computer, i.e., the compiler or interpreter that is processing your code, can check the correctness of the program and allocate the appropriate amount of memory to store the variable. While most modern languages can guess (or infer) the type, declaring types is still good practice because it helps with the readability of the compute code.

Remark 1 (Why do we need Types?)

Types are an essential concept in programming, and they are used to ensure the correctness and efficiency of your code. Modern languages such as Julia and Python have sophisticated type systems that include basic numerical, logical, and text types, and they allow you to create your own types and define how they interact with other types. However, some languages, such as Python, hide the type system from the user, while other languages, such as Julia, expose the type system to the user.

But how are types represented on the computer? At the smallest scale, information is stored as bits and bytes in the computer (Fig. 1)

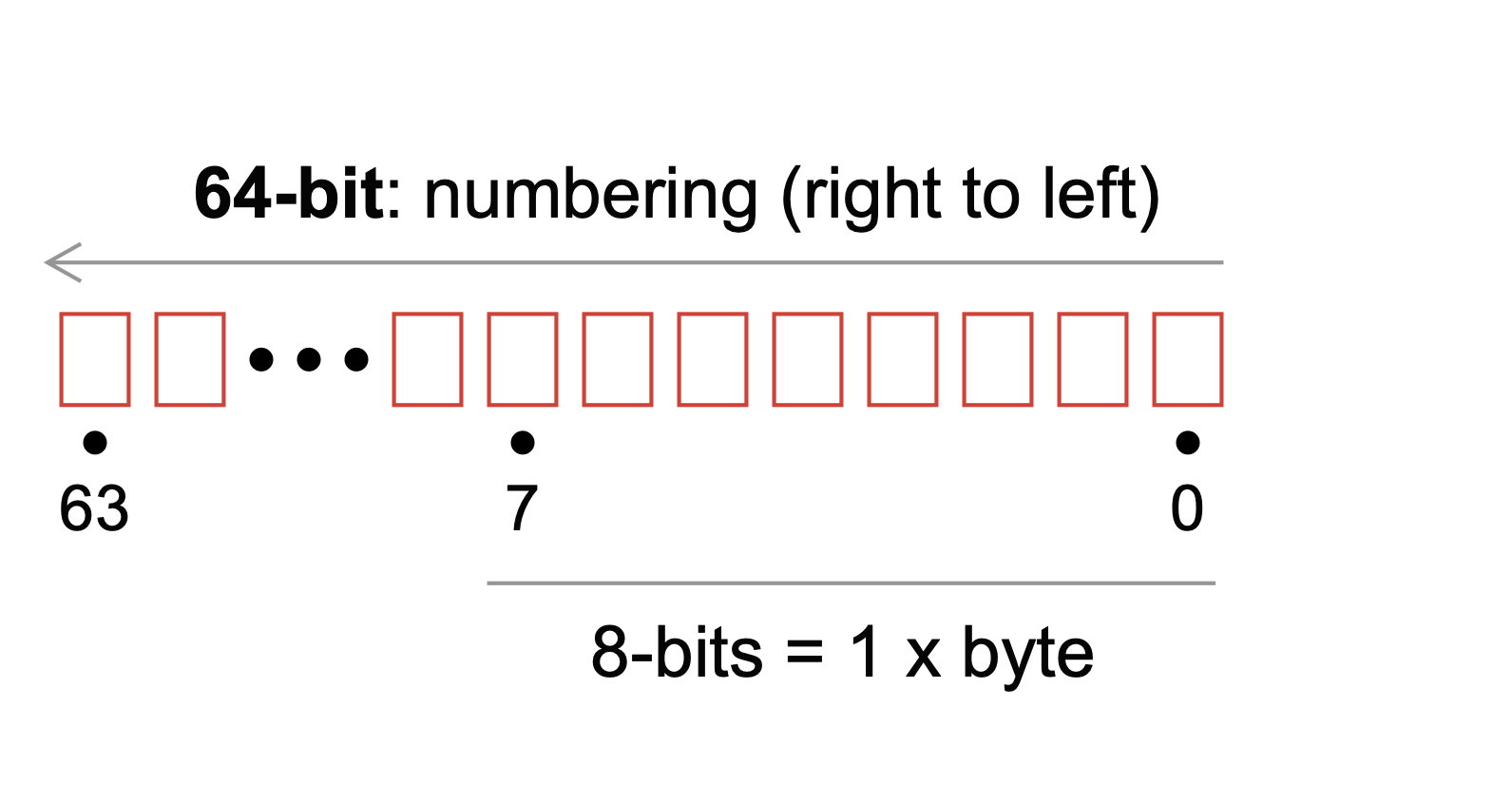
../_images/Fig-64-bit-byte-label-pattern.png

Fig. 1 A schematic of bytes and bits used in computer storage. Each box contains a digit in the numbering system. In a binary system, each box contains a 0 or 1.#

A bit is the smallest unit of storage on a computer; a bit is a 0 or a 1. However, a bit is too tiny for practical computing tasks. Instead, bits are grouped into bytes; a group of 8 bits equals 1 \(\times\) byte. Different types of things, e.g., integers or text, are then represented as different numbers of bytes.

Integers, floating-points, and logical values are the basic building blocks of arithmetic and computation. Built-in representations of these values, i.e., the structure that the computer understands, are called numeric primitives. On the other hand, the models of numbers that humans understand, e.g., integers, floating-point numbers, etc., are called numeric literals, e.g., 1 is an integer literal, and 1.0 is a floating-point literal. Modern programming languages such as Julia and Python provide a broad range of primitive numeric types. Further, many standard mathematical operations are defined over them, e.g., addition, subtraction, and multiplication.

Numeric primitives, which the computer understands, are binary numbers (numbers written to the base 2). However, there are other number systems that you may encounter, e.g., numbers written in the base 8 (octal) or base 16 (hexadecimal) system (Definition 1):

Definition 1 (Base \(\texttt{b}\) numbers)

Let \(k\) denote the \(\texttt{word-size}\) of the computer, i.e., the number of bits in a \texttt{word}. The base \(b\) representation of a number uses the digit set:

\[ \begin{equation} \mathcal{D}_{b} = \left\{0, 1, \dots, (b - 1)\right\} \end{equation} \]

For any \(n\geq{0}\) and \(b\geq{2}\), there is a string of \(k\)-digits \(\left(a_{k-1}\,a_{k-2},\dots,a_{2}\,a_{1}a_{0}\right)_{b}\) where \(a_{i}\in\mathcal{D}_{b}\,\forall{i}\) such that the \texttt{base-10} representation of the number \(n\) is given by:

\[ \begin{equation} n = \sum_{j=0}^{k-1}a_{j}\cdot{b^{j}} \end{equation} \]

where \(a_{j}\) denotes the digit in position \(j\), the quantity \(b\) denotes the base, and \(k\) denotes the number of bits in a \(\texttt{word}\).

Let’s look at an example of a base 8 number (Example 1):

Integers#

Signed integers, represented by the set \(\mathbb{Z}\), are the positive and negative natural numbers along with zero:

\[\mathbb{Z} = \left\{\dots, -3,-2, -1, 0, 1, 2, 3, \dots\right\}\]

The in-memory representation of signed integers, i.e., their numeric primitive representation, is typically a 4 \(\times\) byte (32-bit) or 8 \(\times\) byte (64-bit) binary number; on newer hardware and operating systems, the default value for a signed integer is an 8 \(\times\) byte (64-bit) binary number (Example 2).

Definition 1 shows the representation of numbers in different bases, e.g., integers written in base 2 (binary numbers). However, the set \(\mathbb{Z}\) also contains negative numbers; how can we represent negative integers in a base 2 system?

Negative integers are created using Two’s complement, a method to represent negative integers in binary form. It allows for efficient arithmetic operations, such as addition and subtraction, to be performed on signed numbers. Two’s complement is executed by first inverting all bits, i.e., flipping 0 \(\rightarrow\) 1 and vice-versa, and then adding (using binary addition) a 1 to the least significant digit (far right bit) of the result (Example 3):

Boolean values#

Boolean values, e.g., values of true and false are represented in modern languages using a Bool type. For example, both Julia and Python have built-in Boolean types. However, foundational languages such as the C-programming language do not have a dedicated Boolean type; instead, Boolean values in C were represented by integers, i.e., true = 1 and false = 0. Thus, it should not be surprising that in languages such as Julia, which is a distant relative of C, Bool is implemented as a subtype of integer (a special 8-bit integer).

In Julia, values of the Bool type are a kind of number: false is numerically equal to 0 while true is equivalent to 1. However, unlike an Int64, only 1\(\times\)byte (8-bits) is required to store a Bool value in Julia; because a Bool can only assume one of two possible values the computer doesn’t need to use extra storage:

# These are examples of expressions that set a Bool value
value_true = true
value_false = false

# What is the bitstring that encodes this value?
println("False: $(bitstring(value_false)) and True: $(bitstring(value_true))")

False: 00000000 and True: 00000001

Thus, while a Bool value will evaluate to either 1 or 0:

# This expression sets a Bool value
value_true = true

# Does true evaluate to 1 (the == is a test for equality)?
value_true == 1

true

it requires less storage than an equivalent Int value:

# This expression sets a value of 1 (interesting: how does Julia know this is an Int?)
int_value = 1

# What is the bitstring that encodes this value?
bitstring(int_value)

"0000000000000000000000000000000000000000000000000000000000000001"

Floating point numbers#

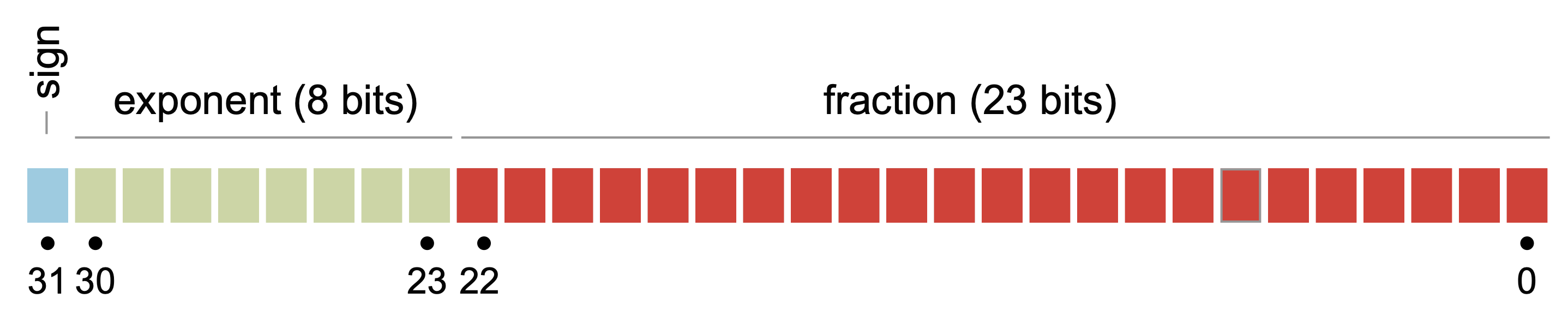
../_images/Fig-Float32-bit-pattern.png

Fig. 2 Schematic of the bit-pattern for a 4\(\times\)byte (32-bit) floating point number#

Floating point numbers \(x\in\mathbb{R}\) are stored using 4\(\times\)bytes (single-precision) or 8\(\times\)bytes (double-precision) following the IEEE-754 standard, where different components of the floating number are encoded in different segments of the 32- or 64-bits (Fig. 2). For a \(\texttt{64-bit}\) float \(x\in\mathbb{R}\), the number is stored as:

\[ \begin{equation} x = -1^{S}\times{M}\times{2}^{(E-1023)} \end{equation} \]

where \(S\) denotes the sign bit, \(M\) denotes the mantissa (fraction) and \(E\) denotes the exponent.

  • For a \(\texttt{32-bit}\) floating point number, \(S\) is \(b_{31}\), \(M\) is encoded in bits \(b_0\rightarrow{b_{22}}\) and \(E\) is encoded by bits \(b_{23}\rightarrow{b_{30}}\).

  • For a \(\texttt{64-bit}\) floating point number, the sign bit \(S\) is \(b_{63}\), \(M\) is encoded by bits \(b_0\rightarrow{b_{51}}\), and \(E\) is encoded by bits \(b_{52}\rightarrow{b_{62}}\). where \(b_{i}\) denotes the \(i\)-th bit in the word, and \(M\) is defined as (for a \(\texttt{64-bit}\) float):

\[ \begin{equation} M = \left(1+\sum_{i=1}^{52}b_{52-i}2^{-i}\right) \end{equation} \]

Let’s consider the representation of a Float64 value for \(\pi\) (Example 4):

Character and String Types#

Textual data on a computer is represented as the String data type. Strings in languages such as C were modeled as a sequence of characters, where each character was type Char. Further, characters were represented via the American Standard Code for Information Interchange (ASCII) system, which was a set of 7-bit teleprinter codes for the AT&T Teletypewriter exchange (TWX) network. For example, the character A in the ASCII system has an index of 65. Later, 8-bit character mappings were developed, i.e., the so-called extended ASCII systems, which had \(0,\dots,255\) possible character values.

However, modern languages use sophisticated built-in String types constructed using the Unicode character set.

  • The Unicode standard encodes approximately 1.1 million possible characters; the first 128 of these are the same as the original ASCII set. Unicode characters, which use up to 4\(\times\)bytes (32-bits) of storage per character, are indexed using the base 16 (hexadecimal) number systems.

Let’s consider the representation of the character J in the ASCII and Unicode systems (Example 5):

Modern languages, such as Julia or Python, have sophisticated built-in String types constructed using the Unicode character set. Strings can be created using double quotes in Julia or single quotes in Python:

# This is an expression to create a string in Julia
string = "Julia strings use double quotes"

# This is an expression to create a string in Python
string = 'Python strings use single quotes. Why python, why?'

However, while the types of characters that can be incorporated into a Julia String is more diverse, in many ways, modern strings share features with the older array representation of text. For example, a Julia (or Python) String can be indexed like an array:

# This is a Julia expression to create a string
string = "Julia strings use double quotes"

# grab a range of characters (from 1 to 5)
println(string[1:5])

Julia

The fragment generated by indexing, e.g., the sequence of characters in the range \(1\rightarrow{5}\) shown above, is also of type String:

# This is an expression to create a string in Julia
string = "Julia strings use double quotes"

# grab a range of characters
fragment = string[1:5]

# what type is the stuff that I just grabbed?
println("The fragment is type -> $(typeof(fragment))")

The fragment is type -> String

If you want (or need) to work with the individual characters in text, you can convert a String type into an Array{Char,1} type using the collect function in Julia:

# This is an expression to create a string in Julia
string = "Julia rocks the house"

# Make an array of characters 
array = collect(string)

21-element Vector{Char}:
 'J': ASCII/Unicode U+004A (category Lu: Letter, uppercase)
 'u': ASCII/Unicode U+0075 (category Ll: Letter, lowercase)
 'l': ASCII/Unicode U+006C (category Ll: Letter, lowercase)
 'i': ASCII/Unicode U+0069 (category Ll: Letter, lowercase)
 'a': ASCII/Unicode U+0061 (category Ll: Letter, lowercase)
 ' ': ASCII/Unicode U+0020 (category Zs: Separator, space)
 'r': ASCII/Unicode U+0072 (category Ll: Letter, lowercase)
 'o': ASCII/Unicode U+006F (category Ll: Letter, lowercase)
 'c': ASCII/Unicode U+0063 (category Ll: Letter, lowercase)
 'k': ASCII/Unicode U+006B (category Ll: Letter, lowercase)
 's': ASCII/Unicode U+0073 (category Ll: Letter, lowercase)
 ' ': ASCII/Unicode U+0020 (category Zs: Separator, space)
 't': ASCII/Unicode U+0074 (category Ll: Letter, lowercase)
 'h': ASCII/Unicode U+0068 (category Ll: Letter, lowercase)
 'e': ASCII/Unicode U+0065 (category Ll: Letter, lowercase)
 ' ': ASCII/Unicode U+0020 (category Zs: Separator, space)
 'h': ASCII/Unicode U+0068 (category Ll: Letter, lowercase)
 'o': ASCII/Unicode U+006F (category Ll: Letter, lowercase)
 'u': ASCII/Unicode U+0075 (category Ll: Letter, lowercase)
 's': ASCII/Unicode U+0073 (category Ll: Letter, lowercase)
 'e': ASCII/Unicode U+0065 (category Ll: Letter, lowercase)

By default, each character in a Julia string requires 4\(\times\)bytes (32-bits) of storage.

Composite types#

Composite types are custom data types made up of one or more other types. Let’s start with two simple composite types: arrays and structs. Later, we’ll consider some additional composite types, e.g., tuples and dictionaries which have unique properties that make them useful for specific tasks. An array is a composite data type that theoretically allows any data to be stored in a sequence of elements. Arrays can be read-only in that they have a fixed size and cannot be modified after they are created, or read-write in the sense that they can be changed after they are made. On the other hand, A struct is a composite data type that allows data to be stored in named fields. Structs can be read-only, i.e., Immutable, or read-write, i.e., Mutable.

You define a struct by using the struct keyword followed by a name for the struct and a list of field names and types. For example, let’s define an immutable Student struct that has a sid and a netid field:

struct Student
    
    # data fields 
    sid::Int64
    netid::String
end

# build an instance -
student = Student(1,"xyz123"); # we pass the required data into the struct as args

A mutable struct is a struct whose fields can be modified after creation. You can create a mutable struct by using the mutable struct keyword instead of struct and by adding a constructor method:

mutable struct Student
    
    # data fields 
    sid::Int64
    netid::String

    # constructor: builds a new empty Student
    Student() = new()
end

# build an empty instance -
student = Student(); # contains no data
student.sid = 1
student.netid = "xyz123" # we add data using the "dot" notation

The struct composite data type contains only data; in the examples above, the Student datatype holds two values, sid is an integer type, and netid is a string type. Except for the special case of the constructor on the mutable Student struct, composite types in Julia do not have functions attached to them.

In other mainstream programming languages, e.g., Python, Java, C++, Ruby, etc composite types also have named functions associated with them, and the combination is called an object. In purer object-oriented languages, such as Ruby or Smalltalk, all values are objects whether they are composites or not. In less refined object-oriented languages, including C++ and Java, some values, such as integers and floating-point values, are not objects, while instances of user-defined composite types are true objects with associated methods. In Julia, all values are objects, but functions are not bundled with the objects they operate on.

Summary#

In this lecture, we introduced expressions, variables, and types. Understanding these is fundamental to writing programs in any programming language.

  • Expressions are combinations of values, variables, and operators that produce a new value when evaluated.

  • Variables are named storage locations that can hold values. They are used to store values that may change during a program’s execution.

  • Types are categories of values, and every value belongs to a specific type. Programming languages have many different types, including primitive types (such as numbers and booleans) and composite types (such as arrays and objects).

Next, we build upon our introduction of expressions, variables, and types and consider some other technical computing build blocks and strategies, namely Functions, Control Statements, and Recursion.

Contents